January 04, 2016

Using Implied Volatility to Predict Equity/ETF Returns

January 04, 2016/ Brian Christopher

During a discussion with an knowledgeable options trader, I was told the significance of interpreting the "Implied Volatility Skew" for stocks and given a paper to read for homework. To get a basic understanding of Implied Volatility Skew see this link here.

The paper I was told to read was "What Does Individual Option Volatility Smirk Tell Us About Future Equity Returns?" by Yuhang Xing, Xiaoyan Zhang and Rui Zhao. In their paper they show empirically, using their SKEW measure, allowed one to predict future stock returns between 1-4 weeks out. Furthermore they also show that a long-short portfolio based on their SKEW measure can generate alphas of 10+% annualized. This their SKEW measure:

Source: What Does Individual Option Volatility Smirk Tell Us About Future Equity Returns?

This idea was very intriguing. Using the Python/Pandas/Yahoo Finance API, I downloaded all the available options data for SPY holdings, and for a selected group of ETF's.

I then used the paper's SKEW measure to sort the equities into deciles. I want to track the performance of some of the highlighted ETF's in the top and bottom deciles in real-time. Here are the resulting names for this week.

ETF SKEW LONGS

XLF

EPI

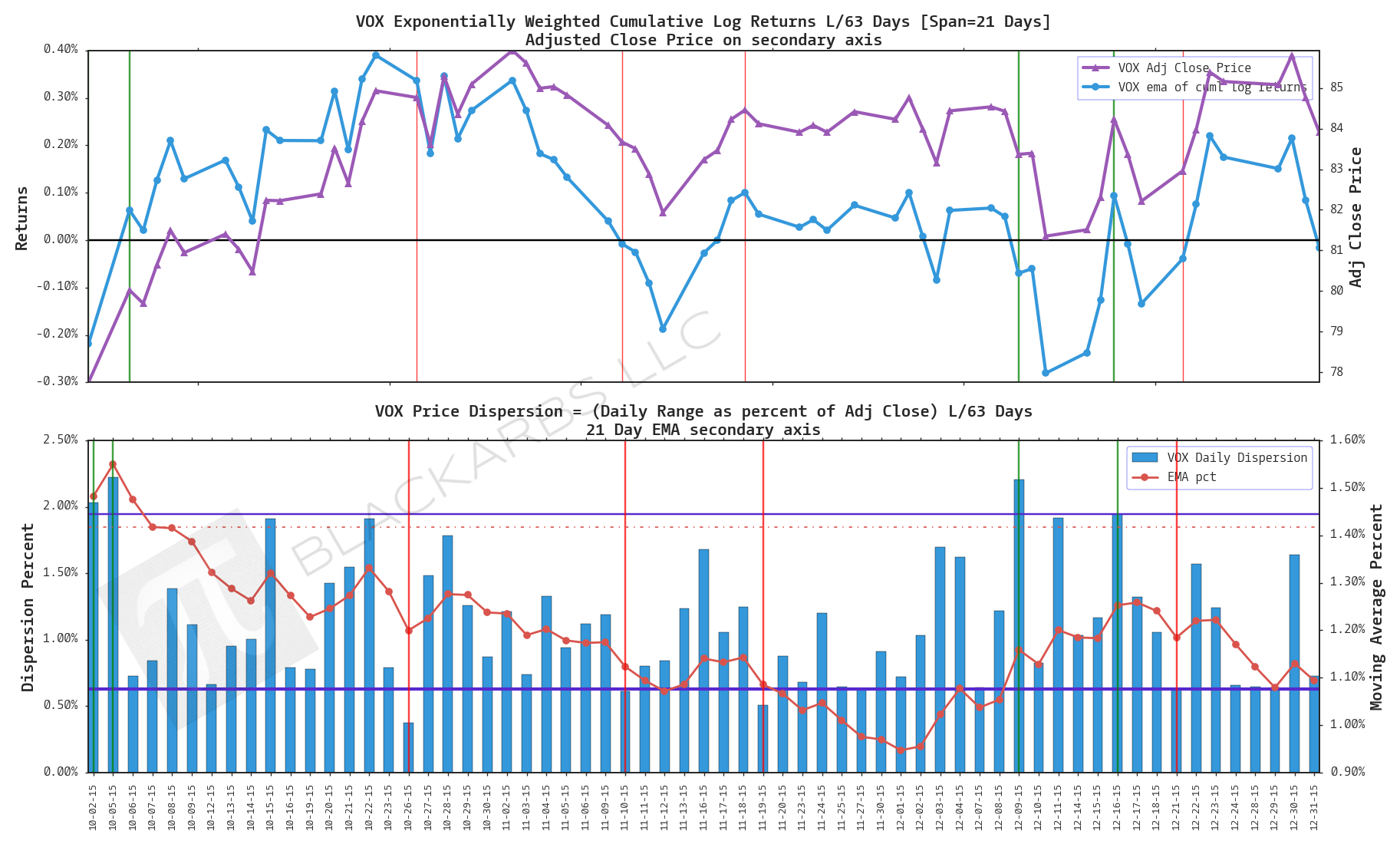
VOX

VOX relative volume + dispersion study L63 Days_01-02-16.png

XLI

XLP

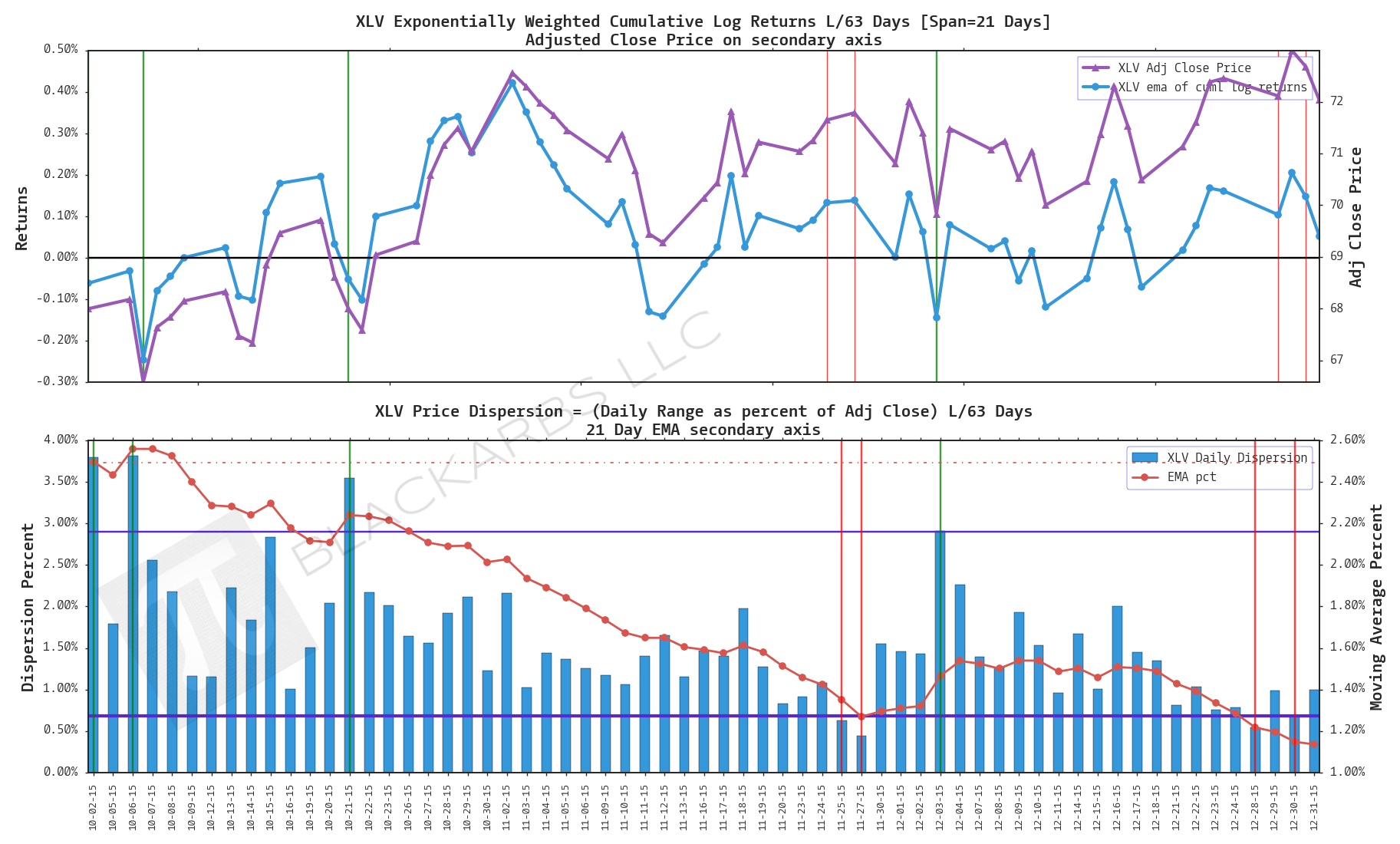
XLV

HEDJ

IYT

etf skew shorts

EZU

XLB

GDXJ

XRT

XHB

VGK

KRE

EWT

December 20, 2015

GET FREE FINANCIAL DATA W/ PYTHON (EARNINGS ESTIMATES-FROM YAHOO FINANCE)

December 20, 2015/ Brian Christopher

Today I present a simple function to extract Earnings Estimates from Yahoo Finance. If you have any questions feel free to leave it in the comments.

This code uses Python 3 on Windows 8.1 but could be easily adapted for Python 2 by changing the 'urllib' import.

First we import the necessary packages into our programming environment.

import pandas as pd
import urllib as u
from bs4 import BeautifulSoup as bs
import warnings
warnings.filterwarnings("ignore")

I also suppress warnings for the deprecation warning for the Pandas "Dataframe.convert_objects()"method within the scraper function that follows.

This function takes the Yahoo Finance URL with our symbol of interest and uses BeautifulSoup to parse the resulting HTML. I also added some formatting code to clean up the readability of the headers.

def _get_eps_estimates(url):
    try:
        html_source = u.request.urlopen(url).read()
        soup = bs(html_source, 'lxml')
        # 
        # table
        table = soup.find_all('table', attrs={'class': 'yfnc_tableout1'})
        header = [th.text for th in table[0].find_all(class_='yfnc_tablehead1')]
        header_title = header[0]
        header_cols = header[1:5]
        index_row_labels = header[-5:]
        body = [[td.text for td in row.select('td')] for row in table[0].find_all('tr')]
        body = body[1:]
        df = pd.DataFrame.from_records(body)
        df = df.ix[:, 1:]
        df.index = index_row_labels
        header_cols = pd.Series(header_cols)
        header_cols = header_cols.str.replace(
            'Year', 'Year ').str.replace('Qtr.', 'Qtr. ')
        df.columns = header_cols
        eps_est = df.convert_objects(convert_numeric=True)
    except Exception as e:
        print(e)
    return eps_est

Now let's test the function using the proper URL. I'm using the symbol 'SWKS' in this example.

symbol = 'SWKS'

base_url = r'http://finance.yahoo.com/q/ae?s={}+Analyst+Estimates'.format(symbol)
eps_est = _get_eps_estimates(base_url)
eps_est

Your output should appear like the following:

October 02, 2015

Could SPY ETF Component Participation Have Alerted Us to Sell (Hedge) Prior to the Recent Market Downturn?

October 02, 2015/ Brian Christopher

This is the Python Code version of a guest post presented here on RectitudeMarket.com. If you would like to read the analysis without the Python code please click the link above.

To market pundits and casual observers the recent correction in equity markets appeared as a surprise. Overall headline economic data was positive at best and mixed at worst. Domestically, capital markets had been looking ‘ok’ while most of the major volatility was taking place abroad in emerging markets, and commodity based economies like China.

That did not stop SPY from collapsing from an August high of $210.56 to an August low of $187.23, or a decline of ~12.5%. We’ve yet to have a daily close above $200 since the drop, even with a dovish Fed delaying the rate rising cycle once again.

As an investor I’m always searching for intuitive indicators that in essence, tip the collective Market’s hand. One indicator that always seemed interesting to me was ‘ETF Participation’.

What is ETF Participation?

There are likely several definitions on the web. For this analysis, I define ETF participation as the number of ETF component stocks’ returns that increase or decrease on a given day. I selected the SPY ETF for this study because SPY is considered by most to be the de-facto US market proxy.

To conduct this analysis I collected SPY holdings data from State Street. I only used a 252 day lookback due to the changing composition of the ETF. The first chart is a simple bar plot that shows the quantity of the current SPY component stocks that had returns above and below zero.

To begin I set up my exploratory research environment within the IPython notebook.

"""Windows 8.1 64bit, Python 3.4, Pandas 0.17"""
import pandas_datareader.data as web
import pandas as pd
pd.set_option('display.precision', 5)
pd.set_option('display.show_dimensions', True)
pd.set_option('display.max_columns', 100)
pd.set_option('display.max_rows', 50)
import numpy as np
from pandas.tseries.offsets import *
import datetime as dt
import os
import time
from pprint import pprint as pp
import matplotlib.pyplot as plt
import matplotlib as mpl
import matplotlib.dates as dates

mpl.rcParams['font.family'] = 'Rambla'
%matplotlib inline
base_size = 11
size=(1.5 * base_size, base_size)

import seaborn as sns
sns.set_style('white', {"xtick.major.size": 3, "ytick.major.size": 3})
flatui = ["#9b59b6", "#3498db", "#95a5a6", "#e74c3c", "#34495e", "#2ecc71", "#f4cae4"]
sns.set_palette(sns.color_palette(flatui, 7))
# =========================================================== #
# filepath management
project_dir = r'C:\\myprojectdir\\'
watermark_path = project_dir + 'mywatermarkpath.png'
spdrs_data_dir = project_dir + r"_SPDR_holdings\\"
# =========================================================== #
# Datetime management  
d = dt.date.today()
# ---------- Days ---------- 
l10 = d - 10 * BDay()
l21 = d - 21 * BDay()
l63 = d - 63 * BDay()
l252 = d - 252 * BDay()
# ---------- Years ---------- 
l252_x2 = d - 252 * 2 * BDay() 
l252_x3 = d - 252 * 3 * BDay() 
l252_x5 = d - 252 * 5 * BDay()
l252_x7 = d - 252 * 7 * BDay() 
l252_x10 = d - 252 * 10 * BDay() 
l252_x20 = d - 252 * 20 * BDay() 
l252_x25 = d - 252 * 25 * BDay() 
 

After setting up my environment I import the SPY ETF holdings data, and perform some small edits to the ticker symbols in order to get stock price data from the Yahoo Finance API. Finally, I run a function to collect price data and return a Pandas Panel.

etf = 'SPY'
etf_holdings = pd.read_excel(spdrs_data_dir + 'holdings-{}.xls'.format(etf.lower()), skiprows=3)
etf_components = etf_holdings[['Identifier', 'Weight']]

def _get_px(sym, start, end):
    return web.DataReader(sym, 'yahoo', start, end)

def _create_symbol_list():
    symbols = etf_components['Identifier'].dropna()
    symbols = symbols.str.replace('.', '-')
    symbols.iloc[-1] = 'SPY' # add SPY to list
    symbols = symbols.sort_values()
    return symbols  

def _get_stock_price_datapanel():
    missing_symbols = []
    panel_data = {}
    for n, sym in enumerate(symbols):
        try:
            panel_data[sym] = _get_px(sym, l252, d)
            print('[ {} ] downloaded || Remaining = {:<.2%} '.format(\
                                         sym, np.round(1 - n/len(etf_components),4) ))
        except Exception as e:
            missing_symbols.append(sym)
            #pp(e)
            pp('...{} symbol missing...'.format(sym))
        finally:
            pass

    num_errors = len(missing_symbols)        
    print('number of missing symbols: {}\nsymbol error rate: {}'.format(\
                                num_errors, np.round(num_errors/len(etf_components),4) )) 
    pp(missing_symbols)
        
    datapanel = pd.Panel.from_dict(panel_data)
    return datapanel

symbols = _create_symbol_list()  
datapanel = _get_stock_price_datapanel()

My output looks like this:

Next I calculate both log returns and cumulative log returns, then isolate and sum the quantity of stocks whose daily returns were greater than or less than 0.0.

last_n = 252
datapanel = datapanel.ix[:,-last_n:,:]

# ------ Log Returns 
cl = pd.DataFrame()
for S in datapanel:
    cl[S] = datapanel[S]['Adj Close']
    
lrets = np.log(cl / cl.shift(1)) 
crets = lrets.cumsum()
# ------ Number of Stocks whose returns gt/lt zero 
sym_gt_zero = (lrets > 0)
sym_lt_zero = (lrets < 0)

lr = lrets.copy()
gt_df = sym_gt_zero
lt_df = sym_lt_zero

gt_label = r'N Stocks Returns $(> 0)$'
lt_label = r'N Stocks Returns $(< 0)$'

lr[gt_label] = gt_df.sum(axis=1)
lr[lt_label] = lt_df.sum(axis=1) * -1

Next I construct a plot function to give an overview of the data collected so far.

def _basic_participation_plot():
    mpl.rcParams['font.family'] = 'Rambla'
    lbl_size = 15
    f, (ax1, ax2) = plt.subplots(nrows=2, figsize=size)
    axes = (ax1, ax2)
    # ----- Date Formatting
    fmt = '%A, %m.%d.%Y'
    dt_txt_fmt = '[{} - {}]'.format((d - last_n * BDay()).strftime(fmt), (d - BDay()).strftime(fmt))    
    
    crets.SPY.plot(ax=ax1, sharex=ax2, label='SPY Returns')
    ax2.bar(lr.index, lr[gt_label].values, width=1, color=sns.xkcd_rgb['neon green'], label=gt_label)    
    ax2.bar(lr.index, lr[lt_label].values, width=1, color=sns.xkcd_rgb['bright red'], label=lt_label)
    ax1.set_title(r'SPY ETF Component Participation L/{} Trading Days'.format(\
                                                        last_n), fontsize=20, fontweight='demi', y=1.02)
    
    for ax in axes:
        ax.legend(loc='upper right', fontsize=lbl_size, frameon=True).get_frame().set_edgecolor('blue')
        dates_rng = pd.date_range(crets.index[0], crets.index[-1], freq='10D')
        plt.xticks(dates_rng, [dtz.strftime('%m-%d-%y') for dtz in dates_rng], rotation=45) 
        ax.xaxis.set_minor_formatter(dates.DateFormatter(''))
        ax.tick_params(axis='both', labelsize=lbl_size)
        
    ax1.set_ylabel('Cumulative Log Returns', fontsize=lbl_size, fontweight='demi')
    ax2.set_ylabel('Quantity of Stocks', fontsize=lbl_size, fontweight='demi')
    ax2.set_xlabel('Date', fontsize=lbl_size, fontweight='demi')        
    plt.axhline(0, color='k')    
    
    im = mpl.image.imread(watermark_path)
    f.figimage(im, xo=-50, yo=-50, origin='upper', alpha=0.125, zorder=10)
    #sns.despine()  
    
    plt.savefig(project_dir + r'_blog_RM_basicSPY_participation_plot_L{} Days_{}.png'.format(\
                                                    last_n, dt_txt_fmt))
    plt.tight_layout()
    
"""Run the function"""    
_basic_participation_plot()    

The chart may look good but it doesn’t tell us a whole lot. We need a way to see the general trends in participation. To do this I decided to use a basic 63 day exponential moving average for both time series.

"""compute exponential moving average"""
gt_ema = pd.ewma(lr[gt_label], span=63, min_periods=5)
lt_ema = pd.ewma(lr[lt_label], span=63, min_periods=5) * -1

def _ema_participation_plot():
    mpl.rcParams['font.family'] = 'Rambla'
    lbl_size = 15
    f, (ax1, ax2) = plt.subplots(nrows=2, figsize=size)
    axes = (ax1, ax2)
    # ----- Date Formatting
    fmt = '%A, %m.%d.%Y'
    dt_txt_fmt = '[{} - {}]'.format((d - last_n * BDay()).strftime(fmt), (d - BDay()).strftime(fmt))    
    
    crets.SPY.plot(ax=ax1, sharex=ax2, label='SPY Returns')   
    gt_ema.plot(ax=ax2, label='EMA of ' + gt_label)
    lt_ema.plot(ax=ax2, label='EMA of ' + lt_label)
    ax1.set_title(r'SPY ETF Component Participation L/{} Trading Days'.format(\
                                                        last_n), fontsize=20, fontweight='demi', y=1.02)
    for ax in axes:
        ax.legend(loc='upper right', fontsize=lbl_size, frameon=True).get_frame().set_edgecolor('blue')
        dates_rng = pd.date_range(crets.index[0], crets.index[-1], freq='10D')
        plt.xticks(dates_rng, [dtz.strftime('%m-%d-%y') for dtz in dates_rng], rotation=45) 
        ax.xaxis.set_minor_formatter(dates.DateFormatter(''))
        ax.tick_params(axis='both', labelsize=lbl_size)
        
    ax1.set_ylabel('Cumulative Log Returns', fontsize=lbl_size, fontweight='demi')
    ax2.set_ylabel('Quantity of Stocks', fontsize=lbl_size, fontweight='demi')
    ax2.set_xlabel('Date', fontsize=13, fontweight='demi')
    im = mpl.image.imread(watermark_path)
    f.figimage(im, xo=-50, yo=-50, origin='upper', alpha=0.125, zorder=10)
    #sns.despine()    
    plt.tight_layout()
    plt.savefig(project_dir + r'_blog_RM_SPY_Components_EMA_participation_plot_L{} Days_{}.png'.format(\
                                                    last_n, dt_txt_fmt)) 
"""Run the plot function"""                                                   
_ema_participation_plot() 

This looks a little more interesting. We can clearly see a general trend that many more stocks were participating to the upside late in 2014 during the strong rebound from the October lows of 2014. Additionally we can see the indecision of market participants throughout the entirety of 2015 as the spread compressed and oscillated. Even more interesting is that the two time series crossed over repeatedly during the period where SPY was testing 52 week highs.

To get a better understanding of the two EMA series I decided to plot the spread between them. I did not attempt to standardize the spread and made no assumptions about whether the spread is mean reverting or random. However, I do believe it crystallizes our naked eye observations from the previous chart.

"""calculate spread between ema time series"""
spread = (gt_ema - lt_ema)

def _plot_raw_spread():
    mpl.rcParams['font.family'] = 'Rambla'
    lbl_size = 14
    f = plt.figure(figsize=size)
    ax = plt.gca()
    # ----- Date Formatting
    fmt = '%A, %m.%d.%Y'
    dt_txt_fmt = '[{} - {}]'.format((d - last_n * BDay()).strftime(fmt), (d - BDay()).strftime(fmt))      
    
    spread.plot(figsize=size, label='Raw EMA Spread')
    ax.set_title(r'SPY ETF Components Raw EMA Spread L/{} Trading Days'.format(\
                                                        last_n), fontsize=20, fontweight='demi', y=1.02)
    ax.legend(loc='upper right', fontsize=lbl_size, frameon=True).get_frame().set_edgecolor('blue')
    dates_rng = pd.date_range(crets.index[0], crets.index[-1], freq='10D')
    plt.xticks(dates_rng, [dtz.strftime('%Y-%m-%d') for dtz in dates_rng], rotation=45) 
    ax.xaxis.set_minor_formatter(dates.DateFormatter(''))
    ax.tick_params(axis='both', labelsize=lbl_size)    
    plt.axhline(0, color='k')
    ax.set_ylabel('Quantity of Stocks', fontsize=lbl_size, fontweight='demi')
    ax.set_xlabel('Date', fontsize=lbl_size, fontweight='demi')
    im = mpl.image.imread(watermark_path)
    f.figimage(im, xo=-50, yo=-50, origin='upper', alpha=0.125, zorder=10)
    #sns.despine()    
    plt.tight_layout()
    plt.savefig(project_dir + r'_blog_RM_SPY_Components_EMA_Spread_plot_L{} Days_{}.png'.format(\
                                                    last_n, dt_txt_fmt))     
"""Run plot function"""    
_plot_raw_spread()

If it wasn’t clear before it definitely is now. Market participants have not been as bullish as previously advertised. The spread was declining as far back as January 2015 and mostly oscillated around zero before breaking below into negative territory around June 2015. In mid August we see the real break which appears to coincide with the aforementioned 12%+ plunge.

Looking at the EMA spread, the zero line appears to be the important psychological support/resistance line. Theoretically the zero line would represent the maximum indecision point of all market participants, so a move above or below the line would indicate increasing conviction in either direction. Therefore it only makes sense to study those zero crossing points a little further.

"""get the datetime index of zero line spread crosses within a tolerance level""" 
crosses = spread[np.isclose(spread, 0, atol=5)].index

def _plot_zero_crosses():
    mpl.rcParams['font.family'] = 'Rambla'
    lbl_size = 14
    
    f, (ax1, ax2, ax3) = plt.subplots(nrows=3, figsize=size)
    axes = (ax1, ax2, ax3)
    # ----- Date Formatting
    fmt = '%A, %m.%d.%Y'
    dt_txt_fmt = '[{} - {}]'.format((d - last_n * BDay()).strftime(fmt), (d - BDay()).strftime(fmt))    
    
    crets.SPY.plot(ax=ax1, sharex=True, label='SPY Returns')
    gt_ema.plot(ax=ax2, label='EMA of ' + gt_label)    
    lt_ema.plot(ax=ax2, label='EMA of ' + lt_label)
    spread.plot(ax=ax3, label='Raw_EMA_Spread')
    ax1.set_title(r'SPY ETF Component Participation L/{} Trading Days'.format(\
                                                        last_n), fontsize=20, fontweight='demi', y=1.02)
    for ax in axes:
        axymin, axymax = ax.get_ylim()
        ax.set_autoscaley_on(False)
        ax.vlines(crosses, ymin=axymin, ymax=axymax, color='g', linestyle='-', alpha=0.4)        
        ax.legend(loc='upper left', fontsize=lbl_size, frameon=True).get_frame().set_edgecolor('blue')
        dates_rng = pd.date_range(crets.index[0], crets.index[-1], freq='10D')
        plt.xticks(dates_rng, [dtz.strftime('%Y-%m-%d') for dtz in dates_rng], rotation=45) 
        ax.xaxis.set_minor_formatter(dates.DateFormatter(''))
        ax.tick_params(axis='both', labelsize=lbl_size)

    ax1.axhline(0, color='k')
    ax3.axhline(0, color='k')
    
    ax1.set_ylabel('Cumulative Log Returns', fontsize=lbl_size, fontweight='demi')
    ax2.set_ylabel('Quantity of Stocks', fontsize=lbl_size, fontweight='demi')
    ax3.set_ylabel('Quantity of Stocks', fontsize=lbl_size, fontweight='demi')
    ax3.set_xlabel('Date', fontsize=13, fontweight='demi')
    im = mpl.image.imread(watermark_path)
    f.figimage(im, xo=-50, yo=-50, origin='upper', alpha=0.125, zorder=10)
    #sns.despine()    
    plt.tight_layout()
    plt.savefig(project_dir + r'_blog_RM_SPY_Components_EMA_participation_Multiplot_L{} Days_{}.png'.format(\
                                                    last_n, dt_txt_fmt))    
"""Run plot function"""    
_plot_zero_crosses()  

This chart plots vertical lines at each zero crossing for the Raw EMA Spread. Again the chart appears to reinforce my previous theory that market participants have been largely indecisive regarding overall market direction as expressed through ETF component participation.

However, that’s not enough information to make a decision about whether we should have been alert to an impending decline. We need a quantitative method to really drill down into this theory.

To quantify this analysis and add structure to the theory I constructed a simple model. Assuming the zero line is an important psychological barrier, I calculated the subsequent cumulative return over N number of days following each instance of the spread crossing zero. I then calculated the average cumulative return for each N day look ahead period.

The lookahead periods I chose were 1, 2, 3, 5, 10, and 21 days. The results are unambiguous.

def _cumlrets_given_trigger(trigger_dates, look):
    '''function to calculate cumulative returns given a date and lookahead period'''
    cr = {}
    for date in trigger_dates:
        start_int = lrets.SPY.index.get_loc(date)
        start = lrets.SPY.index[start_int]
        end = start + look * BDay()
        cumlrets = lrets.SPY.ix[start:end].cumsum().iloc[-1]
        cr[date] = cumlrets 
    conditional_rets = pd.Series(cr, index=cr.keys(), \
                                 name='_{} days lookahead_'.format(look)).sort_index()
    return conditional_rets

def _get_avgrets_bylook(trigger_dates):
    '''function to aggregate cumulative returns given a date and lookahead period'''
    lookahead = [1, 2, 3, 5, 10, 21]
    rets_dict = {}
    avg_returns_looks = {} 
    for look in lookahead:
        rets = _cumlrets_given_trigger(trigger_dates, look)
        mean_rets = rets.mean()
        avg_returns_looks['{}_Days'.format(look)] = mean_rets
        rets_dict['{}_Days'.format(look)] = rets

    avg_rets_looks = pd.Series(avg_returns_looks, index=avg_returns_looks.keys(),\
                               name='_avg_returns_given_lookahead_')
    avg_rets_looks = avg_rets_looks[['{}_Days'.format(str(i)) for i in lookahead]]
    return avg_rets_looks, rets_dict   
    
"""looking at the average"""
avg_crets, avgdict = _get_avgrets_bylook(crosses)
print(avg_crets)

Current average cumulative returns are negative across all look ahead periods!

Notice a pattern? Looking at the table the trend appears to change for all look ahead timeframes in late May. It never got better. Obvious confirmation of the near term trend change could be seen as late as the end of July 2015.

Conclusions

Circling back to the original question, analyzing the SPY ETF components’ participation gave clear indications that broad market internals were weakening as early as late May, and continued to break down until present day.

Unfortunately, market internals still appear weak moving forward. For my personal portfolio, I would not feel confident as a long term dip buyer until ETF participation crosses over the zero line again and we see some positive cumulative returns accumulating on the 10 and 21 day periods.

This analysis provides a good foundation for further research regarding this indicator’s effectiveness. However there are some weaknesses to consider. The rolling EMA periods were chosen simply to represent a quarterly period but were largely arbitrary as were the lookahead periods. Furthermore, I did not have access to SPY ETF components ‘as of’ each date in the analysis which would have been more rigorous and largely eliminated the survivorship and look-ahead bias. Therefore, I only analyzed the last 252 trading days to minimize those effects on the results presented.

September 21, 2015

Guest Post Previously Featured on RectitudeMarket.com (09/02/2015)

September 21, 2015/ Brian Christopher

**Note: This post already appeared as a guest post on rectitudemarket.com. The reason I'm posting this article when it is 'outdated', is twofold. 1) I think it's beneficial to review previous works especially when one has the benefit of hindsight. This helps us determine the accuracy and bias of the research presented. 2) I further introduce the concept of conditional cumulative returns, which adds insight to what happens to our securities' returns given some other event occurring. In this case, the event is simply whether our benchmark ETF's cumulative returns are rising or falling during some period.

Are There Any Equity Industry Groups Outperforming During this Recent Market Volatility?

Stock market volatility has picked up in a big way. It has been some time since market participants have experienced consecutive 2-4% up/down moves in the major market averages. The selling has been broad based and market sentiment has deteriorated as well.

With this backdrop I wondered if any industry groups were doing well. By doing well I mean 1) relative outperformance when compared to other industries 2) absolute performance greater than zero.

To answer this question I collected all the NYSE and Nasdaq symbols (~3300 symbols), filtered them for firms with a market cap greater than $300 million then I grouped them by industry. I dropped any industries with less than 10 stock symbols. With the filtered dataset I ran the analysis.

First I examined the cumulative return momentum over various lookback periods. Then I examined which industry groups had the best cumulative return performance given a benchmark ETF’s returns are rising (declining).

The benchmark ETF’s I selected for comparison are (SPY, QQQ, VTI).

Unfortunately there are no industry groups with absolute cumulative return performance greater than zero over the last quarterly period (Last 63 Trading Days).

In fact you'd have to back out to view industry group performance Year-to-Date, to find any industry groups with positive cumulative returns. Those industries are: Biotechnology: Commercial Physical & Biological Research, Medical/Nursing Services, Forest Products, and Movies/Entertainment.

To examine relative conditional performance, I selected the top 5% of industry group cumulative return performance given increasing benchmark returns (Last 63 Trading Days)

Focusing on SPY, the strongest performers given increasing returns have been: Finance: Consumer Services, Investment Bankers/Brokers/Service, Investment Managers, and Clothing/Shoe/Accessory Stores. Clearly financial firms’ returns are highly sensitive to the performance of SPY. Somewhat surprisingly Clothing/Shoe/Accessory Stores have outperformed given increasing returns in all 3 benchmark ETFs.

For long only investors, unfortunately there are no industries which have recorded positive absolute cumulative return performance given a decline in benchmark returns. The best one can hope for is to find industries that decline less than peers during periods of negative market returns.

During the last quarter (Last 63 Trading Days) the best industry performance given declining returns in SPY are: Life Insurance, Auto Parts 0.E.M., Computer Software: Prepackaged Software, and Business Services. I find it surprising that Business Services would be a relative outperformer for all 3 benchmark ETFs.

Another item of note is precious metals being a relative outperformer if VTI returns are declining. I think this makes sense given that VTI is representative of the entire domestic equity market, therefore negative returns in this index is more likely to induce catastrophe hedges and/or ‘panic trades’.

If your portfolio has been hit during this period of heightened volatility take solace in knowing you are not alone. No industry is safe. However, all is not lost, by creating a shopping list of your favorite quality names now on discount, you can be ready to strike with conviction when the proper opportunity presents itself.

August 27, 2015

Was David Woo Right; Was the Selloff Exacerbated by Risk Parity Strategies?

August 27, 2015/ Brian Christopher

Today after the close Bloomberg TV had David Woo, Managing Director and Head of Global Rates and Currencies Research at Bank of America/Merrill Lynch, on to provide some insight regarding recent market action. More specifically, he addressed how Chinese and American markets are linked.

He dropped a lot of gems during his segment but one point really struck a chord with me. He said that the recent selloff has likely been exacerbated by "Risk Parity Guys".

If you're unfamiliar with 'risk parity' here are some good working definitions:

“Risk parity (or risk premia parity) is an approach to investment portfolio management which focuses on allocation of risk, usually defined as volatility, rather than allocation of capital.”

— https://en.wikipedia.org/wiki/Risk_parity

“A portfolio allocation strategy based on targeting risk levels across the various components of an investment portfolio. The risk parity approach to asset allocation allows investors to target specific levels of risk and to divide that risk equally across the entire investment portfolio in order to achieve optimal portfolio diversification for each individual investor. ”

— http://www.investopedia.com/terms/r/risk-parity.asp

Essentially, this says that risk parity strategies approach portfolio allocation based on the underlying asset's risk/volatility as opposed to traditional portfolio allocation which allocates capital based on holding some specified amount of each asset class.

David Woo went on to elaborate that traditional asset class correlations began to break down during this selloff, implying that traditional methods of diversification were no longer viable and as a result any fund/fund manager which allocates capital on the basis of 'risk parity' or similar strategies would be forced to reduce risk across all asset classes.

I thought this was a brilliant insight and immediately wanted to see if I could find some evidence that would support his analysis.

To do this I used my Composite ETF model to plot rolling correlations of the 'Bonds' ETF composite vs the ETF composite of each asset class. The reason I use rolling correlation is because of the inherent link between asset correlations and volatility. Specifically, as correlations across assets/asset classes rise diversification decreases and volatility/tail risk increases. I've selected some of the more interesting plots that lend credence to his statement.

bonds vs asia-pac equity

bonds vs consumer discretionary

bonds vs consumer staples

bonds vs europe equity

bonds vs financials

bonds vs global equity

bonds vs industrials

bonds vs large cap

bonds vs materials

bonds vs mid cap

bonds vs precious metals

bonds vs real estate

bonds vs small cap

bonds vs telecom

After reviewing some of the evidence I would say David Woo is on to something. To be fair however, rising correlations among this many asset classes over a short time period is likely to cause multiple types of fund strategies to reduce risk exposures quickly.

If you haven't seen his segment I'd recommend trying to find it. Either way I'll be on the lookout for his analysis going forward.

Blog