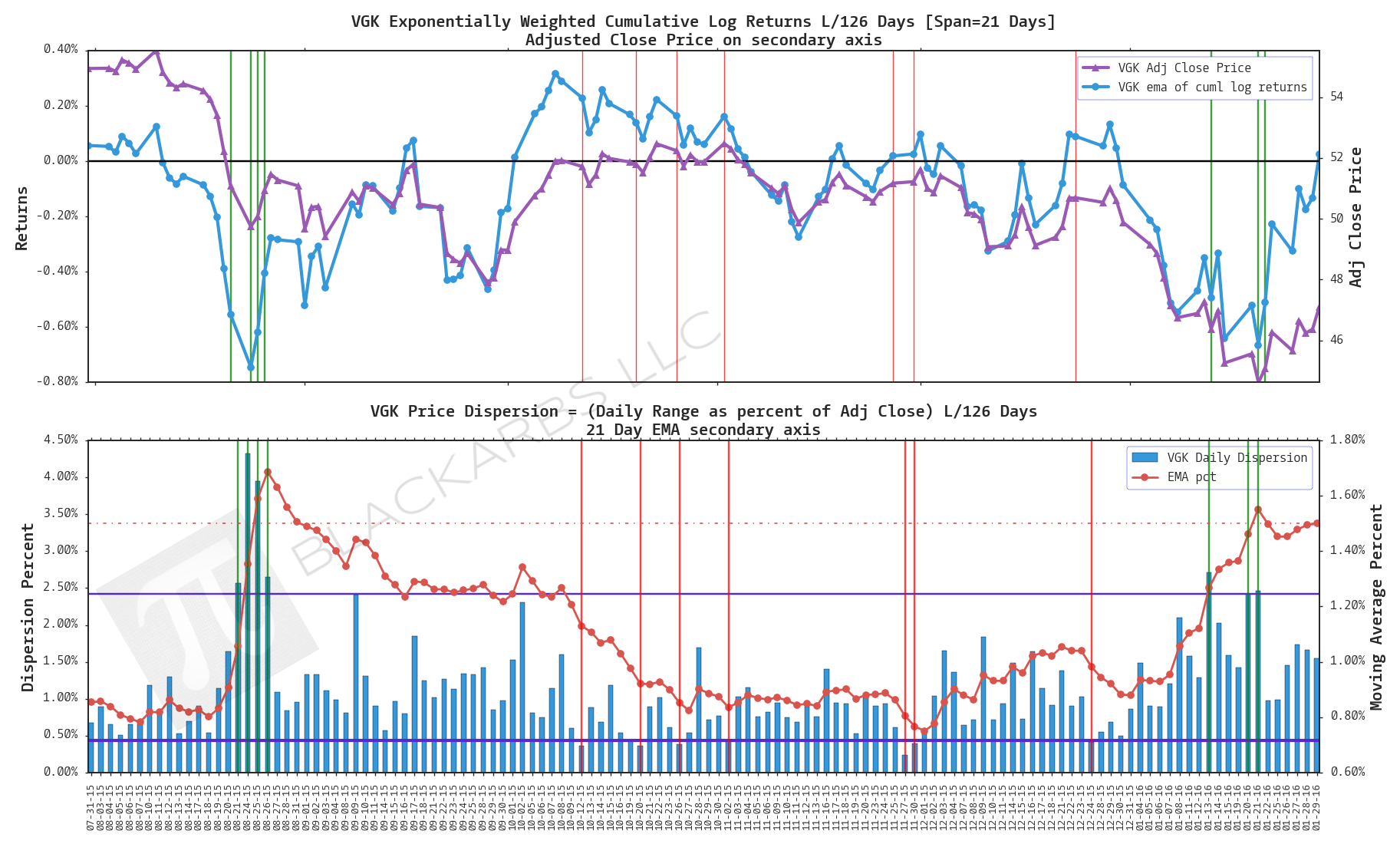
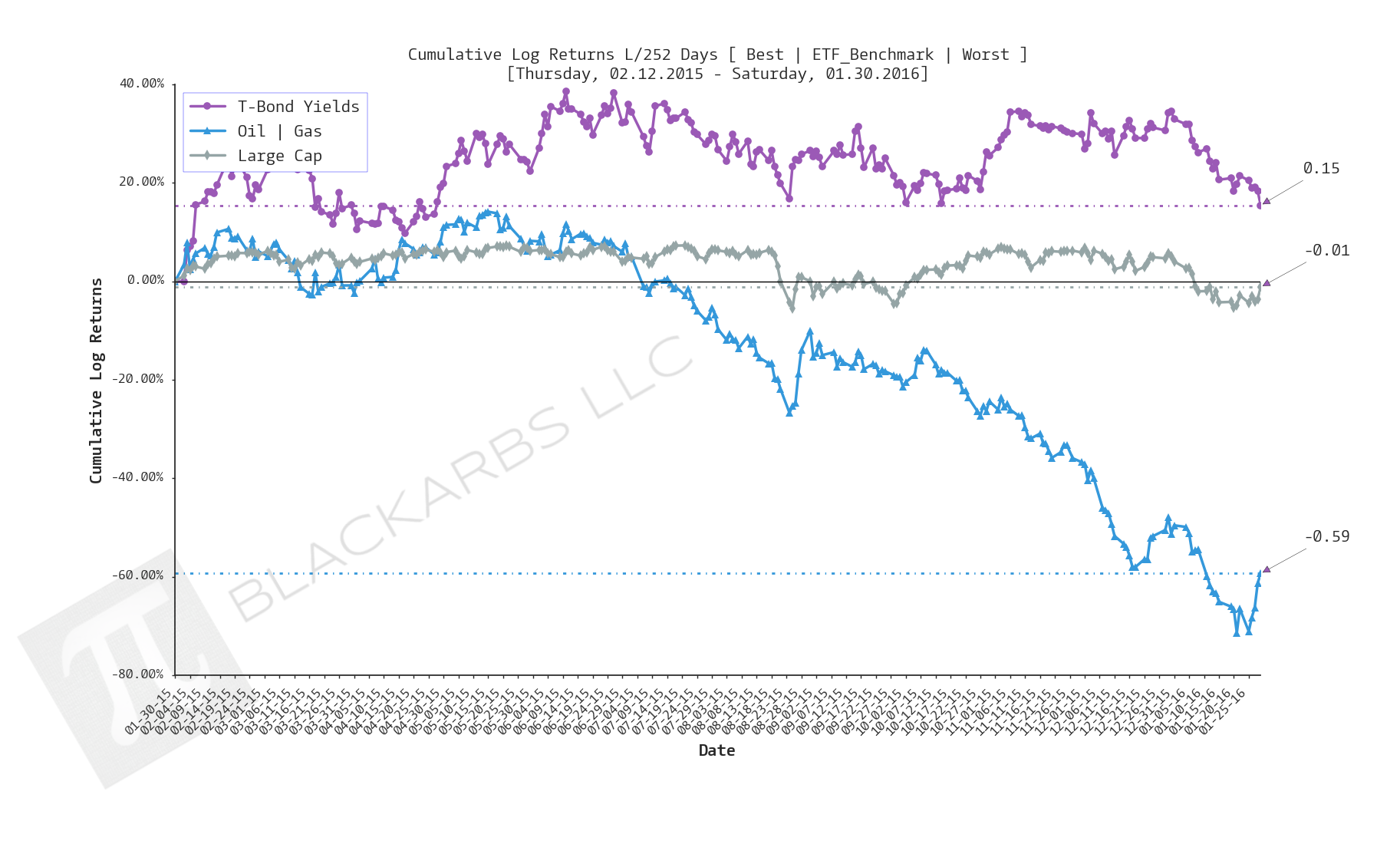
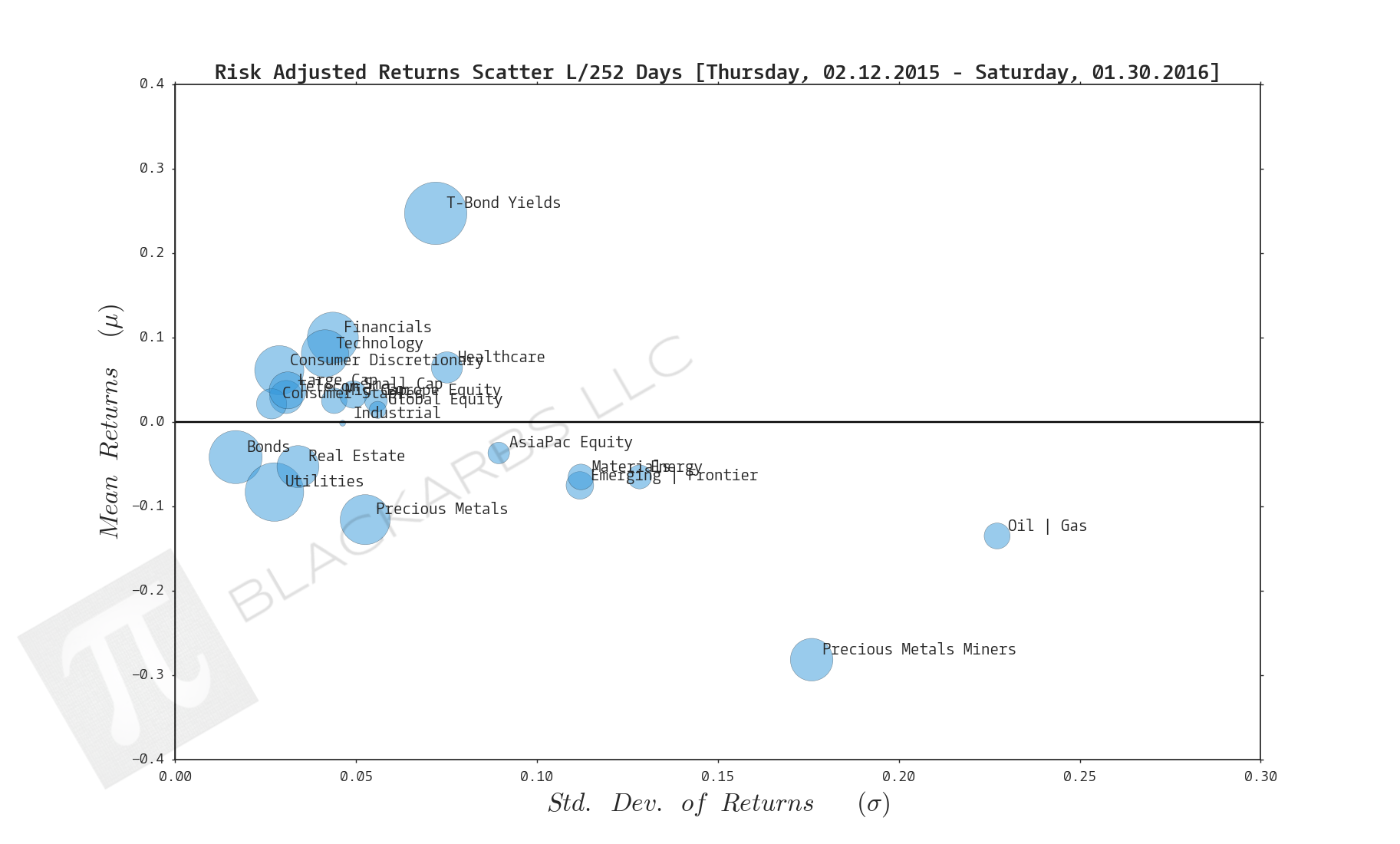
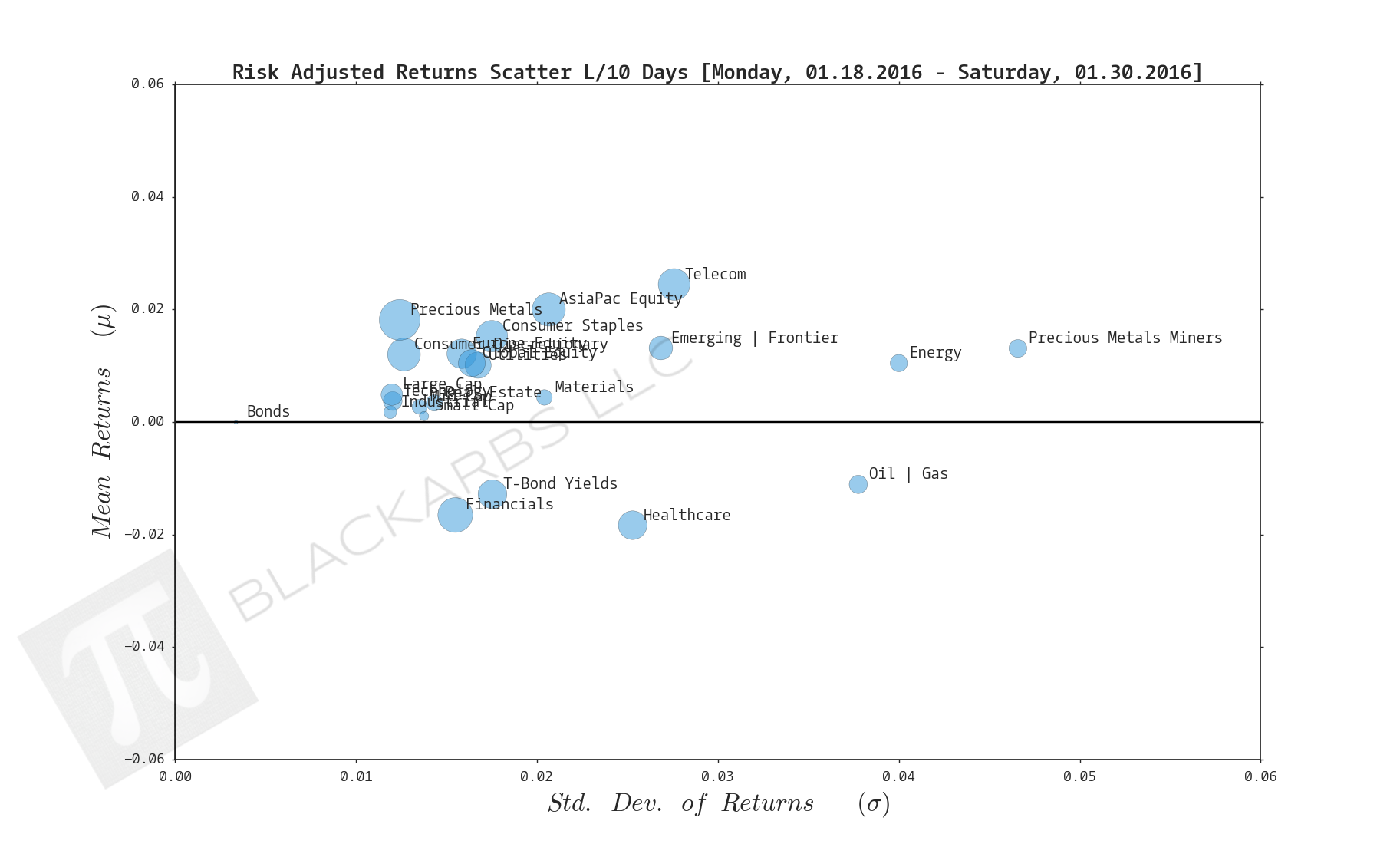
COMPOSITE MACRO ETF WEEKLY ANALYTICS (2/06/2016)

/

FOR A DEEPER DIVE INTO ETF PERFORMANCE AND RELATIVE VALUE SUBSCRIBE TO THE ETF INTERNAL ANALYTICS PACKAGE HERE

LAYOUT (Organized by Time Period): 

  1. Composite ETF Cumulative Returns Momentum Bar plot

  2. Composite ETF Cumulative Returns Line plot

  3. Composite ETF Risk-Adjusted Returns Scatter plot (Std vs Mean)

  4. Composite ETF Risk-Adjusted Return Correlations Heatmap (Clusterplot)

  5. Implied Cost of Capital Estimates

  6. Composite ETF Cumulative Return Tables

  7. Notable Trends and Observations

COMPOSITE ETF COMPONENTS:

LAST 252 TRADING DAYS

LAST 126 TRADING DAYS

LAST 63 TRADING DAYS

LAST 21 TRADING DAYS

LAST 10 TRADING DAYS

Implied Cost of Capital Estimates:

To learn more about the Implied Cost of Capital see here.

CATEGORY AVERAGE ICC ESTIMATES

ALL ETF ICC ESTIMATES BY CATEGORY

Cumulative Return Tables:

Notable Observations and Trends:

  • Market crash risk is rising. What is currently a correction is showing the potential to become much worse.
  • T-Bond Yields are the worst performers over the last 21 and 10 day periods. Recall that Bond yields and prices have an inverse relationship, meaning that Treasury Bonds are seeing a strong bid from the market.
  • Precious Metal Miners and Precious Metals have been among the top 3 performers for 3 out of 5 time periods starting over the last 126 days. These composites are usually bid up as a form of crash protection when investors fear 1) systematic devaluation of the USD and other major currencies 2) global market crash.
  • Utilities being among the top 3 performers across all time periods also support the rising crash risk that markets appear to be pricing in.

For a deeper dive into ETF performance and relative value subscribe to the ETF Internal Analytics package here

Implied Volatility Skew Strategy Mid-Week Update Using Python (2/03/2016)

/

To see this weekend's prediction click here.

Overall this strategy has been impressive in its trial run over the last 4.5 weeks. I figured, given the volatility and uncertainty in the broad markets this week I'd like to see a mid-week update of the strategy using Python and the BarChart OnDemand API. To see my original article on the basics of using the BarChart OnDemand API click here.

First I import the basic modules needed to execute the script:

from copy import copy
import pandas as pd
import pandas_datareader.data as web
from pandas.tseries.offsets import *

From there I define a couple convenience functions. The first is a one off function for querying the BarChart API for singular symbol names. The other is a bulk function to aggregate the portfolio symbol price data into a HDF5 format for easy querying later on.  Remember the api key is your api key.

# ================================================================== #
def _get_barChart_px(sym):
    start = '20160201'
    freq = 'minutes' 
    api_url = construct_barChart_url(sym, start, freq, api_key=apikey)  
    csvfile = pd.read_csv(api_url, parse_dates=['timestamp'])
    csvfile.set_index('timestamp', inplace=True)
    csvfile.index = csvfile.index.tz_localize('utc').tz_convert('US/Eastern')
    return csvfile
# ================================================================== #
def construct_barChart_url(sym, start_date, freq, api_key=apikey):
    '''Function to construct barchart api url'''    
    url = 'http://marketdata.websol.barchart.com/getHistory.csv?' +\
            'key={}&symbol={}&type={}&startDate={}'.format(api_key, sym, freq, start_date)
    return url
   
# ================================================================== #
def get_minute_data(syms):
    '''Function to retrieve minute data for multiple stocks'''
    print('Running Get Minute Data')
    # This is the required format for datetimes to access the API
    # You could make a function to translate datetime to this format
    start = '20160201'
    #end = d
    freq = 'minutes'    
    symbol_count = len(syms)
    N = copy(symbol_count)
    try:
        for i, sym in enumerate(syms, start=1):
            api_url = construct_barChart_url(sym, start, freq, api_key=apikey)
            try:
                csvfile = pd.read_csv(api_url, parse_dates=['timestamp'])
                csvfile.set_index('timestamp', inplace=True)
                # convert timestamps to EST
                csvfile.index = csvfile.index.tz_localize('utc').tz_convert('US/Eastern')
                symbol_store.put('{}'.format(sym), csvfile, format='table')
            except:
                continue
            N -= 1
            pct_total_left = (N/symbol_count)
            print('{}..[done] | {} of {} symbols collected | percent remaining: {:>.2%}'.format(sym, i, symbol_count, pct_total_left)) 
    except Exception as e: 
        print(e)
    finally:
        pass

Next I run the function for aggregating the portfolio stocks prices. 

longs = ['VO', 'GDX', 'XHB', 'XLB', 'HACK', 'XLY', 'XLP', 'XLU']
shorts = ['ACWI', 'VWO', 'IYJ', 'VB', 'VPU', 'ECH', 'VGK', 'IWB']

today = pd.datetime.today().date()
symbol_store = pd.HDFStore(price_path + 'Implied_Volatility_ETF_Tracking_{}.h5'.format(today.strftime('%m-%d-%y')))

symbols = longs+shorts
get_minute_data(symbols)
symbol_store.close()

After aggregating the data I perform some simple clean up operations along with calculation of the mid-prices for each minute of available data. 

'''grab data from our previously created hdf5 file using keys'''
data = {}
loc = price_path + 'Implied_Volatility_ETF_Tracking_{}.h5'.format(today.strftime('%m-%d-%y'))
with pd.HDFStore(loc, 'r') as DATA:
    for key in DATA.keys():
        data[key] = DATA[key]
dat = pd.Panel.from_dict(data) # convert Python Dict to Pandas Panel        

'''construct minute mid-prices'''
mids = pd.DataFrame()
for symbol in dat:
    mids[symbol] = (dat[symbol]['open'] + dat[symbol]['close']) / 2

'''Remove unnecessary forward slash from default HDF5 key label'''
cols = []
for sym in mids.columns:
    symz = sym.replace('/','')
    cols.append(symz)

mids.columns = cols
mids.head()

Because each ETF did not record a trade for every minute I perform a forward fill of the previous price before calculating the log returns. Then I calculate the cumulative sum of the the returns for both the long and short legs of the portfolio for comparison. 

mids = mids.ffill()
lrets = np.log(mids / mids.shift(1))

crets = lrets.cumsum()
last_cret = crets.ix[-1]

long_rets = pd.Series()
for long in longs:
    long_rets.loc[long] = last_cret.loc[long]
    
short_rets = pd.Series()
for short in shorts:
    short_rets.loc[short] = last_cret.loc[short]

Finally, we arrive at the moment of truth. How has the strategy performed for the first 3 trading sessions of the week?

net_gain = long_rets.mean() - short_rets.mean()
print('long positions mean return: {:.3%}\nshort positions mean return: {:.3%}\ngross strategy pnl: {:.3%}'.format(long_rets.mean(), short_rets.mean(), net_gain))

Not bad at all! How does that compare to the US Major Market Averages? I perform almost the same process for the SPY, QQQ, and DIA ETF's except I use the singular BarChart API function defined above. I also calculate the mid-price for each minute of data. 

'''get price data from BarChart'''
spy = _get_barChart_px('SPY')
qqq = _get_barChart_px('QQQ')
dia = _get_barChart_px('DIA')

'''calculate the midprice'''
spy_mid = (spy['open'] + spy['close']) / 2
qqq_mid = (qqq['open'] + qqq['close']) / 2
dia_mid = (dia['open'] + dia['close']) / 2

'''calculate the returns'''
spyr = np.log(spy_mid / spy_mid.shift(1))
qqqr = np.log(qqq_mid / qqq_mid.shift(1))
diar = np.log(dia_mid / dia_mid.shift(1))

'''calculate the cumulative sum of the returns'''
spyc = spyr.cumsum().ix[-1]
diac = diar.cumsum().ix[-1]
qqqc = qqqr.cumsum().ix[-1]

print('spy returns: {:.2%}\ndia returns: {:.2%}\nqqq returns: {:.2%}\nstrategy gross return: {:.2%}'.format(spyc, diac, qqqc, net_gain))

Wow! Not even close.

USING IMPLIED VOLATILITY TO PREDICT ETF RETURNS (1/30/16)

/

To see the origin of this series click here

In the paper that inspired this series ("What Does Individual Option Volatility Smirk Tell Us About Future Equity Returns?") the authors' research shows that their calculation of the Option Volatility Smirk is predictive of equity returns up to 4 weeks. Therefore, each week, I will calculate the Long/Short legs of a portfolio constructed by following their criteria as closely as possible. However this study will focus on ETF's as opposed to single name equities. I will then track the results of the Long/Short portfolio, in equity returns, cumulatively for 4 weeks before rotating out of that portfolio. The ETF's are selected from the following groups:

PORTFOLIO ONE

Longs: XLF, EPI, VOX, XLI, XLP, XLV, HEDJ, IYT

Shorts: EZU, XLB, GDXJ, XRT, XHB, VGK, KRE, EWT

Week 1, Week 2, Week 3, Week 4 and Cumulative Results: 

PORTFOLIO TWO

Longs: VPU, IJR, FEZ, IWB, INDA, HEDJ, IYT

Shorts: LQD, EWW, IAU, VDE, EWT, EEM, EWH

Week 1, Week 2, Week 3 and Cumulative Results:

PORTFOLIO THREE

Longs: VWO, KRE, XLU, EEM, HEDJ

Shorts: EWW, HACK, JNK, XLP, IYR

Week 1, Week 2 and Cumulative Results:

PORTFOLIO FOUR

Longs: XRT,  XLY,  XLP,  XHB,  GDXJ,  IYT,  XME,  MDY

Shorts: EPI, XLU, HEDJ, JNK, EWQ, VEU, XLI

Week 1 Results:

PORTFOLIO FIVE

Longs: VO, GDX, XHB, XLB, HACK, XLY, XLP, XLU

Shorts: ACWI, VWO, IYJ, VB, VPU, ECH, VGK, IWB

ETF SKEW LONGS

VO

GDX

XHB

XLB

HACK

XLY

XLP

XLU

ETF SKEW SHORTS

ACWI

VWO

IYJ

VB

VPU

ECH

VGK

IWB


COMPOSITE MACRO ETF WEEKLY IMPLIED COST-OF-CAPITAL ESTIMATES VS. CUMULATIVE RETURNS (1/30/16)

/

WHAT IS THE "IMPLIED COST OF CAPITAL (ICC)" MODEL?

“In accounting and finance the implied cost of equity capital (ICC)—defined as the internal rate of return that equates the current stock price to discounted expected future dividends—is an increasingly popular class of proxies for the expected rate of equity returns. ”

— CHARLES C. Y. WANG; an assistant professor of business administration in the Accounting and Management Unit at Harvard Business School

The basic concept of the ICC model is that it is a forward looking estimate of the implied earnings growth rate of stock given the current stock price. It is calculated using a combination of equity book value and earnings forecasts.

To see a more involved explanation of the previous model I used see here.  

In the past I used a Multi-Stage Residual Income Model. However, this time around I've decided to use a simpler Single-Stage Residual Income Model for these estimates. I chose this because I believe the additional complexity is not warranted given my purpose which I will elaborate on further.

The Single-Stage Residual Income Model as defined by the CFA Institute is the following:

source: CFA Institute

'V' is the stock price at time 0, 'B' is the book value of equity at time 0, 'ROE' is return on equity, 'g' is an assumed long term growth rate and 'r' is the cost of equity/capital. The ICC model essentially solves for 'r' given the other inputs. 

WHY USE THE IMPLIED COST OF CAPITAL MODEL?

There is ongoing debate regarding the ICC model's application and accuracy as a proxy for expected returns as quoted by Charles C. Y. Wang. As an investor/trader I'm less interested in the academic debate and more intrigued by the intuition behind the model and its practical application as a relative value tool. 

I use the ICC model as a relative value measure to identify analyst/institutional expectations and sentiment between different market sectors at a point in time. 

For this purpose I believe it provides great insight. 

COMPOSITE ETF COMPONENTS FOR ICC ESTIMATES

Z-SCORE ICC ESTIMATES AND CUMULATIVE RETURNS COMPARISON CHART

The below plot gives visual representation of the ICC estimates. I z-scored both year-to-date cumulative returns and the ICC estimates so we can view them on the same scale. Examining this chart allows investors to quickly determine which market sectors are outperforming (underperforming) their respective Implied Cost of Capital Estimates. 

The extreme cases show where there are disconnects between the analyst community's forward earnings expectations and actual market performance. The plot is sorted left to right by ascending ICC estimates.

LAST 252 TRADING DAYS 

Data Sources: YCharts.com, Yahoo Finance

Data Sources: YCharts.com, Yahoo Finance

LAST 126 TRADING DAYS

Data Sources: YCharts.com, Yahoo Finance

Data Sources: YCharts.com, Yahoo Finance

LAST 63 TRADING DAYS

Data Sources: YCharts.com, Yahoo Finance

Data Sources: YCharts.com, Yahoo Finance

LAST 21 TRADING DAYS

Data Sources: YCharts.com, Yahoo Finance

Data Sources: YCharts.com, Yahoo Finance

LAST 10 TRADING DAYS

Data Sources: YCharts.com, Yahoo Finance

Data Sources: YCharts.com, Yahoo Finance

CATEGORY AVERAGE ICC ESTIMATES

Long term growth rate (g) is assumed to be 2.5% reflective of our low growth high debt economic environment.

ALL ETF ICC ESTIMATES BY CATEGORY

COMPOSITE MACRO ETF WEEKLY ANALYTICS (1/30/2016)

/

LAYOUT (Organized by Time Period): 

  1. Composite ETF Cumulative Returns Momentum Bar plot

  2. Composite ETF Cumulative Returns Line plot

  3. Composite ETF Risk-Adjusted Returns Scatter plot (Std vs Mean)

  4. Composite ETF Risk-Adjusted Return Correlations Heatmap (Clusterplot)

  5. Composite ETF Cumulative Return Tables

  6. Notable Trends and Observations

COMPOSITE ETF COMPONENTS:

LAST 252 TRADING DAYS

LAST 126 TRADING DAYS

LAST 63 TRADING DAYS

LAST 21 TRADING DAYS

LAST 10 TRADING DAYS

Cumulative Return Tables:

Notable Observations and Trends:

  • Last 10 days provides strong evidence of a relief rally as all but 2 composites showed positive cumulative gains. Further evidence is the leadership group comprised of Energy, Precious Metals Miners, and Emerging/Frontier which had been heavily oversold on a long and medium term basis.
  • Additionally over the Last 10 days one of the worst 3 performers (Bonds) had positive performance.
  • Telecom has emerged as a composite to watch being one of the top 3 performers over the last 252 days. Perhaps it is the new safe haven asset class as it has been a top 5 performer on all time frames under study.
  • Telecom has also been a strong performer on a risk-adjusted basis seemingly hugging the belly of the efficient frontier, near or above zero, across all time frames.